7.1. Процедуры решения многоцелевых задач
Почти всякая сложная техническая задача принятия решения многоцелевая, т.к. при выборе наилучшего варианта приходится учитывать много различных требований, предъявляемых к машине, и среди этих требований встречаются противоречащие друг другу. Однако почти все математические методы оптимизации предназначены для нахождения экстремума одной функции - т.е. для одной цели. Поэтому чаще всего пытаются свести многоцелевую задачу к одноцелевой [11,c.30-37]. Эта процедура в большинстве случаев приводит к серьезному искажению существа проблемы и, следовательно, к неоправданной замене одной задачи другой.
Если при решении одноцелевых задач методологических проблем не возникает, а возможны только вычислительные трудности, то иначе обстоит дело с многоцелевыми решениями. Здесь основные нюансы связаны со следующей проблемой: что следует считать наилучшей альтернативой в задаче с несколькими целевыми функциями, которые противоречивы и достигают максимума в различных точках множества альтернатив? На этот счет на сегодняшний день не существует единого мнения, поэтому оценка качества системы в случае векторного показателя качества является одной из главных проблем в теории эффективности и исследования операций.
Многомерные цели могут находиться друг с другом в следующих отношениях:
Если цели частично нейтральны, частично кооперированы и частично конкурируют между собой, то задача формулируется таким образом, что нужно принимать во внимание только конкурирующие цели. Рассмотрение нейтральных или кооперативных целей не представляет особых трудностей, так что проблемы, ориентированные на множество целей, прежде всего должны быть рассмотрены в части конкурирующих целей, коль скоро все они вместе не могутбыть выражены одномерным параметром.
Можно предложить следующую структуру существующих на сегодняшний день процедур решения такого рода многоцелевых задач:
В известной степени эти методы переплетаются друг с другом, поэтому данная структура не претендует на законченный вид, а способствует лучшему пониманию путей решения рассматриваемой в работе проблемы.
7.2. Априорные процедуры многоцелевой оптимизации и соответствующие им методы принятия решения
В процедурах априорного типа делается явное или неявное предположение, что вся информация, позволяющая определить наилучшее решение, скрыта в формальной модели задачи и, следовательно, с помощью некоторых преобразований может быть из этой формальной модели извлечена и использована. т.е. считается, что множеств альтернатив U и целевых функций W1(u), W2(u),
... вполне достаточно для объективного, не зависящего от отсутствующих в данной модели факторов определения оптимального решения.Рассмотрим ряд методов, суть которых заключается сведении задачи к одноцелевой.
Метод главной компоненты заключается в том, что критерий качества связывается с одним из показателей, выбранных в роли основного (главного). На основные показатели накладываются ограничения. В этом случае по главному показателю реализуется критерий оптимальности, по остальным - пригодности
. Например, если имеется вектор полезного эффекта в видеW<k> = <W1, W2, ... Wk>, (7.1)
где
Wi(i=1,2...k) - компоненты вектора, например, для машины: производительность, экологичность, надежность, себестоимость и т.д., то метод главной компоненты заключается в произвольном выборе одного из компонентов в качестве главного, по которому производится оптимизация и выбирается решение. При этом остальные компоненты переводятся в разряд ограничений.
Этот метод прост, нагляден и часто применяется в машиностроительной практике, однако принципиальным его недостатком является произвол в выборе главного критерия. Можно привести много примеров из истории науки и техники, когда произвольный и неверный выбор этого критерия приводит к трагическим последствиям или, по меньшей мере, к малоэффективным результатам.![]()
В литературе, посвященной вопросам оптимизации программ рубок ухода, в качестве главного показателя выбирают, например, их себестоимость или объем лесопользования [37], [30], [33]). При оптимизации металлоконструкций лесных машин - металлоемкость [2,3], [11], [35]). Когда решаются технологические задачи лесного производства принято использовать в качестве главной компоненты производительность [38], [36]).
Для задач, у которых критерии не равнозначны, применяется другой метод решения - уступок. Прежде чем решать поставленную задачу по методу уступок, необходимо:
Пример 7.1.
Решить задачу по двум критериям, считая наиболее предпочтительным. Его отклонение от максимального значения составляет 10 %:W1 = x1 + 2 x2 (r) max;
W1 = x1 + 2 x2 (r) min;
x1 + 2 x2 і 6;
x1 Ј 4;
x2 Ј 5;
x1 і 0; x2 і 0.
Решая задачу линейного программирования по первому показателю эффективности W1, например в среде пакета EXCEL или графически, получаем, что максимальное значение целевой функции W1* = 14 достигается при x1 = 4 и x2 = 5. Делаем уступку на 10%, т.е. уменьшаем величину W1* = 14 до значения W1** = 14Ч 0,9 = 12,6. Вносим в задачу дополнительное ограничение
x1 + 2 x2 і 12,6.
Далее, решая задачу линейного программирования при минимизации второго показателя эффективности имеем W2* = 7,6 при x1 = 2,6 и x2 = 5. При этом значение показателя эффективности W1 не изменилось и равно 12,6.
Метод комплексного критерия, в отличие от метода главной компоненты, применяется довольно редко. Он заключается в переходе от векторного критерия к скалярному путем образования суммарного монопоказателя. При этом основная идея метода заключается в составлении одной функции, аргументами которой служат компоненты вектора полезного эффекта. Особенно частым случаем является представление такой функции в виде дроби, где в числителе стоят все величины, увеличение которых желательно (например, эффект), а в знаменателе те, которые хотелось бы уменьшить. В лесной экономике особенно часто, например, употребляется показатель приведенных затрат, где числитель выражает производительность труда (м3), а знаменатель - затраты. Такой показатель в настоящее время подвергается обоснованной критике, так как при этом вводится неявное допущение о том, что недостаток в одном показателе может быть скомпенсирован за счет другого. При этом, если желательно не оговаривать условия, то может получиться, что комплекс дорогостоящих, но и высокопроизводительных машин (харвестер + форвардер) будет иметь одинаковый показатель с каким-нибудь устаревшим вариантом, имеющим малую производительность и, соответственно, стоимость.
Другим, несколько более замысловатым методом составления комплексного критерия является метод его свертывания (метод Гермейера).
В этом методе комплексный критерий образуется в виде следующего произведения.
Пусть каждый критерий Wi(u) характеризует некоторый показатель изделия альтернативы u - металлоемкость, производительность, грузоподъемность, надежность, устойчивость, доступность предмета труда, повреждаемость древостоя, вибронагруженность оператора. Наилучшая альтернатива, по-видимому, характеризуется наиболее удачным сочетанием всех этих показателей качества, т.е. имеет максимальное значение "глобального" качества. Таким образом, для выбора наилучшей альтернативы достаточно уяснить, каким образом глобальное качество зависит от единичных показателей качества, после чего многоцелевая задача может быть сведена к задаче скалярной оптимизации с использованием функции вида:
![]() , (7.2)
, (7.2)
где
l
i - коэффициент значимости i-го показателя качества. ОбычноЭтот метод можно применять, если достаточно точно известны l i. Обычно l i определяются с помощью метода экспертных оценок или на основании хорошо апробированных статистических данных.
Здесь основная трудность заключается в способе назначения коэффициентов значимости. Обычно для их определения используют экспертные методы. Поэтому в ряде ситуаций может употребляться модель, в которой глобальное качество альтернативы представляет собой сумму единичных показателей (принцип равномерной оптимальности) [39]:
![]() . (7.3)
. (7.3)
Этой моделью пользуются в задачах, в которых критерии имеют одну и ту же единицу измерения (как правило, стоимостную). В качестве примера можно привести целевую функцию лесоводственно-экономического обоснования оптимального размера промежуточного пользования, предложенную Мошкалевым А.Г. [40].
Если критерии Wi(u) не выражаются в одних и тех же единицах измерения, то их приводят к безразмерному виду путем деления значения каждого критерия на единицу соответствующего масштаба или путем введения функции [39]:
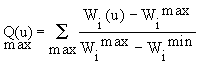 , (7.4)
, (7.4)
где
Wimin и Wimax - соответственно минимальное и максимальное значения критериев качества на допустимом множестве.
Основным недостатком принципа равномерной оптимальности является невозможность компенсации недопустимо малых значений некоторых критериев достаточно большими значениями других.
Действительно, если u характеризует проект манипулятора, а W1 и W2 представляют собой надежность и грузоподъемность, то он может обладать очень высокой надежностью в том случае, когда сможет (в лучшем случае) поднять из-за чрезмерного собственного веса лишь собственный захват или харвестерную головку. Очевидна бесполезность такого изделия, глобальное качество которого может быть довольно большим, если определять его по принципу равномерной оптимальности.
Свободен от этого недостатка метод справедливого компромисса:
![]() (7.5)
(7.5)
Как видно из формулы, манипулятору с нулевой грузоподъемностью будет присвоено нулевое значение. Этот принцип оптимальности весьма популярен и встречается во многих работах.
Методы компромиссов в большей степени приспособлены к решению задач в векторной постановке [3].
Метод условного центра масс нашел довольно широкое распространение в лесотехнических приложениях. В работах [1-8], [12], [15] на основе этого метода решены задачи обеспечения эффективности лесохозяйственных машин для рубок ухода, лесомелиоративных агрегатов, гидроманипуляторов трелевочных машин.
Пусть последовательно найдены значения экстремумов для каждого показателя Wi(u), что соответствует точкам в пространстве параметров с координатами {x1i*, x2i*,..., xni*}.
Введем понятие "условной массы" точки [3]:
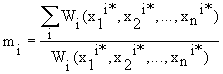 , (7.6)
, (7.6)
где
Wi(x1i*, x2i*,..., xni*) - значение i-го показателя эффективности при совокупности управляемых параметров, обеспечивающих экстремальное его значение. Будем полагать, что компромиссному решению будет удовлетворять набор параметров, соответствующих точке с координатами "условного центра масс":
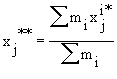 . (7.7)
. (7.7)
Найденные по этому методу средневзвешенные значения параметров xi** учитывают не только интересы всех показателей качества, но и чувствительность каждого по отношению к данному параметру.
Завершим обзор априорных процедур рассмотрением метода идеальной точки в пространстве критериев [41,42]. Пусть на множестве альтернатив U заданы n целевых функций W1(u),...,Wn(u).
В пространстве векторных оценок рассмотрим идеальную точку x={x1,...,xn}, где xi=minWi(u). Если бы точка x принадлежала множеству векторных оценок, т.е. если бы существовала альтернатива u*О U такая, что Wi(u*) = xi, i = 1,...,n) то, очевидно, что u* была бы лучшей альтернативой. Однако, как правило, этого не происходит, поэтому в качестве наилучшей альтернативы предполагается выбрать такую точку, векторная оценка которой находится ближе всего к идеальной точке x.
Интуитивно такой подход представляется очень привлекательным. Однако он не лишен довольно существенных недостатков. Одни из основных - возникновение проблемы выбора метрики и несоответствие аксиоме независимости.
Как показано выше, ни один из перечисленных выше методов не свободен от недостатков, связанных с желанием упростить задачу и сделать ее однозначной. Однако, как правило, упрощение сложного явления, в принципе не упрощаемого, не может дать верного ответа.
Поэтому, в настоящее время разработан ряд методов, не "уходящих" от сложности проблемы и предпочитающих учитывать все ее стороны. Такие методы основаны на принципе компромисса, то есть принятия взвешенного решения, в котором фигурируют в определенной пропорции все действующие факторы. При этом, в некоторых методах предлагается не однозначный ответ а лишь область разумных (рациональных) решений. Принятие же однозначного решения остается прерогативой лица принимающего решение (ЛПР). Одним из таких методов является весьма распространенный метод Парето, предложенный итальянским математиком-экономистом Парето в 1904 году. Основная идея метода Парето заключается в сохранении множества возможных вариантов и выделении области из которой необходимо выбирать наиболее целесообразные варианты. При этом к области Парето относится только такое множество решений, где с изменением какого-либо из них критерии меняются противоречиво. Поясним более подробно это положение.
Предположим, что принято некоторое решение x*, которому соответствует значение критерия Wi(x*) [i=1...n]. Затем в результате исследований (оптимизации) получено другое решение x**, для которого
"
Wi(x**)і Wi(x*). (7.8)Очевидно, что решение
x* целесообразно исключить из рассмотрения. К области Парето относятся только такие решения, для которых не существует такого x**, чтобы для всех критериев удовлитворялись неравенства (4. ).Более ясным это условие становится при рассмотрении следующего графика (см. рис. 7.1).
Предположим, что целью исследований является
W1(x)(r) max, W2(x)(r) max,
где
W1, W2 - какие либо критерии;
x - решение (выбор).
Построим гипотетический график зависимости wi(x), рис.7.1.
|
W2(x) a b d
c e W1(x) |
|
Рис.7.1. Выделение области Парето |
Из предыдущих рассуждений следует, что к области парето относятся только участки
a-b и d-e, так как:Необходимо отметить, что построение области Парето является трудно формализируемой задачей, так как при этом необходимо проводить многократно трудоемкий процесс оптимизации. Однако Н.Н.Моисеевым предложен сравнительно простой и наглядный графоаналитический метод приближенного построения области Парето.
Метод Н.Н. Моисеева заключается в последовательном итеративном процессе решения простейших оптимизационных задач. При этом сначала задаются начальными произвольными значениями критериев:
W1(o)=C1; W2(o)=C2. Затем решаются две оптимизационные задачи:Решив эти две задачи находят точки a и b (рис.4.2).
Прямая, соединяющая эти две точки является областью Парето в первом приближении. Далее решаются две аналогичные задачи. При этом задаются значениями критериев: W1(o)=C3; W2(o)=C4. Затем решаются две оптимизационные задачи:
Через полученные точки снова проводят прямые. После соединения точек
c и d получают ломаную acdb, которая является областью Парето второго приближения. В большинстве случаев второе приближение является достаточным.В случае большего числа критериев метод теряет наглядность, но может выполняться с помощью ЭВМ.
При решении задач указанным выше методом существует одно принципиальное затруднение. Оно связано с тем, что множество Парето не всегда может оказаться выпуклым. В этом случае этим методом пользоваться нельзя и необходимо использовать другими методами решения компромиссных задач.Метод зондирования с помощью ЛП
t - последовательности. Анализ всех предшествующих методов принятия решений показывает, что всем им присущи те или иные недостатки, связанные с попытками формализации в принципе неформализуемой задачи. В этом случае напрашивается решение, использующее идею полного просмотра всех возможных вариантов решений и выбора из них лучшего. Однако, естественно, что такой полный просмотр невозможен, т.к. количество точек просмотра бесконечно. Для того, чтобы уменьшить количество просматриваемых точек можно (конечно, в ущерб получаемого объема информации) каким-либо разумным способом организовать процедуру просмотра. На этой идее и основан метод решения проектно-конструкторских задач с противоречивыми критериями, предложенный И.М.Соболем и Р.Б.Статниковым и основанный на утверждении, что максимальное число просматриваемых точек при минимуме вычислений достигается, если точки выбираются из так называемой ЛПt - последовательности. Название ЛПt - последовательность появилось как сокращение фразы "бесконечные последовательности точек, любой двоичный участок которых есть Пt сетка. Таким образом, просматривая варианты в точках, соответствующих ЛПt - последовательности и, вычисляя значения критериев в этих точках можно принимать эффективные решения.Рассмотрим более подробно порядок решения задач в этом случае. Пусть проектируемая система зависит от
n варьируемых параметров u=(u1,u2,...,un) в n-мерном пространстве. На параметры накладываются функциональные и областные ограничения.Задача решается в диалоговом режиме и состоит из следующих этапов:Остановимся более подробно на порядке выполнения этих этапов.
uij=u*j+qij(u**j-u*j), j=1,2,...,n (7.8)
По точке
u=ui проверяются ограничения. Если они выполнены, то точка u=ui отбирается в качестве пробной и по ней вычисляются значения критериев W. В противном случае пробная точка отбрасывается.Вычисление координат точек
Qi может проводиться с помощью матрицы направляющих числителей (табл. 7.2).Таблица 7.1
|
j\l |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 |
1,0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
2 |
1,25 |
3 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
3 |
0,25 |
1 |
9 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
4 |
1,25 |
3 |
9 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
5 |
1,0 |
1 |
9 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
6 |
0,25 |
2 |
9 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
7 |
0,25 |
1 |
1 |
17 |
1 |
1 |
1 |
1 |
1 |
1 |
|
8 |
1,25 |
3 |
1 |
17 |
1 |
1 |
1 |
1 |
1 |
1 |
|
9 |
1,0 |
1 |
1 |
17 |
1 |
1 |
1 |
1 |
1 |
1 |
|
10 |
0,25 |
2 |
1 |
17 |
1 |
1 |
1 |
1 |
1 |
1 |
|
11 |
0,25 |
2 |
9 |
17 |
1 |
1 |
1 |
1 |
1 |
1 |
|
12 |
1,0 |
1 |
9 |
17 |
1 |
1 |
1 |
1 |
1 |
1 |
|
13 |
1,25 |
3 |
9 |
17 |
1 |
1 |
1 |
1 |
1 |
1 |
|
14 |
0,25 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
513 |
|
15 |
0,25 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
513 |
По таблице числителей
tlj вычисляются координаты vlj направляющих точек vlvlj = tlj 2-l, (7.9)
где
j - номер координаты соответствующей точки P t сетки, l соответствует номеру точки, равному 2l. Если в двоичной системе номер точки Qi i=em,...e2,e1, то координаты этой точки будут
qij = e1v1j* e1v1j*...*e1v1j , (7.10)
где
*
- означает поразрядное сложение по модулю 2 в двоичной системе.Выбор критериальных ограничений. Этот этап предполагает участие ЛПР, который на основании анализа результатов расчета
W назначает критериальные ограничения, если это необходимо.Анализ результатов и принятия решения. На этом этапе анализируются полученные значения
W с учетом всех принятых ограничений. Если все условия выполняются, то находится решение, при котором минимизируется значение показателя эффективности (критерия). В противном случае могут быть пересмотрены критериальные ограничения, т.е. сделаны уступки. На этом этапе решаются еще две важные задачи:W[k,m]=| | rk,m| | , (7.11)
где
rk,m- коэффициент парной корреляции между критериями Wk и Wm;
В заключение отметим следующие моменты. Процедуры данного типа основаны на предположении о возможности априорного определения наилучшего соотношения между требованиями, предъявляемыми различными критериями. Понятно, что такая возможность существует не всегда. Кроме того, выбор конкретного вида глобальной функции цели не может быть осуществлен в отрыве от решаемой задачи.
7.3. Апостериорные процедуры многоцелевой
оптимизации и соответствующие им методы
принятия решения
В основе апостериорных процедур лежит предположение, что формальная модель многоцелевой задачи не содержит информации, достаточной для однозначного выбора наилучшей альтернативы. Следовательно, решения, принимаемые с помощью апостериорных процедур, имеют принципиально субъективный характер, что предопределяет необходимость привлечения субъективных суждений конструктора. Учет предпочтений проектанта в этом случае является одним из наиболее эффективных методов снятия имеющейся неопределенности.
Апостериорные процедуры принятия решений заключаются в формулировке дополнительных требований, накладываемых на предпочтения проектанта, выполнение которых позволяет однозначно восстановить некоторую скалярную функцию полезности P(u), после чего задача принятия решений сводится к скалярной оптимизации.
Типичная структура апостериорной процедуры решения многокритериальных задач такова. Сначала выполняется проверка гипотезы о независимости по полезности. Если ответы проектанта позволяют сделать вывод, что независимость действительно имеет место, то с помощью специальных методов (часто используется принцип лотереи) восстанавливаются все величины, необходимые для идентификации искомой функции полезности.
Основным достоинством апостериорных процедур по сравнению с априорными является четкое определение условий, при выполнении которых ими можно пользоваться. Но их практическое использование часто наталкивается на необходимость сбора чрезвычайно большого количества информации, а также на то, что проектант во многих случаях либо не может дать информацию, необходимую для реализации процедуры, либо дает ее с большими ошибками. Это связано, как правило, с неподготовленностью проектанта к решению такого рода задач.
7.4. Адаптивные процедуры многоцелевой оптимизации
и соответствующие им методы принятия решения
Как известно, в кибернетике под адаптацией понимается "процесс накопления и использования информации в системе, направленный на достижение определенного, обычно оптимального в некотором смысле состояния или поведения системы при начальной неопределенности или изменяющихся внешних условиях [174]. Из приведенного выше определения в результате анализа можно сформулировать некоторые общие принципы адаптации:
В процессе адаптации (адаптивного управления) могут меняться: параметры, структура системы, алгоритм функционирования, управляющие воздействия и т.д. Как известно, процесс оптимального проектирования может интерпретироваться в виде задачи оптимального управления. Поэтому к нему могут быть полностью применены как общие принципы, так и методы адаптации. При этом адаптация здесь может рассматриваться с двух точек зрения:
7.5. Контрольные вопросы и задания
с1 x1 + с2 x2 (r) max,
d1 x1 + d2 x2 (r) min,
a11 x1 + a12 x2 і b1;
a21 x1 + a22 x2 Ј b2;
a31 x1 + a32 x2 Ј b3;
a41 x1 + a42 x2 Ј b4 ;
x1 , x2 і 0.
Таблица 7.2.
|
Ва ри ан |
Элементы вектора ресурсов |
Вид сруба |
|||||||||||||||
|
т |
|
|
|
|
1 |
2 |
|||||||||||
|
|
b1 |
b2 |
b3 |
b4 |
с1 |
d1 |
a11 |
a21 |
a31 |
a41 |
с2 |
d2 |
a21 |
a22 |
a32 |
a42 |
|
|
0 |
12 |
10 |
6 |
7 |
3 |
2 |
3 |
1 |
1 |
0 |
5 |
1 |
1 |
4 |
0 |
1 |
|
|
1 |
24 |
20 |
3 |
3 |
2 |
1 |
12 |
4 |
1 |
0 |
4 |
1 |
3 |
4 |
0 |
1 |
|
|
2 |
6 |
4 |
5 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
2 |
1 |
2 |
0 |
1 |
0 |
|
|
3 |
14 |
11 |
5 |
6 |
3 |
2 |
3 |
1 |
1 |
0 |
5 |
1 |
1 |
4 |
0 |
1 |
|
|
4 |
12 |
10 |
6 |
7 |
3 |
2 |
3 |
1 |
1 |
0 |
5 |
1 |
1 |
4 |
0 |
1 |
|
|
5 |
23 |
19 |
3 |
3 |
2 |
1 |
11 |
5 |
1 |
0 |
4 |
1 |
3 |
4 |
0 |
1 |
|
|
6 |
5 |
3 |
4 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
2 |
1 |
2 |
0 |
1 |
0 |
|
|
7 |
14 |
11 |
5 |
6 |
3 |
2 |
3 |
1 |
1 |
0 |
5 |
1 |
1 |
4 |
0 |
1 |
|
|
8 |
24 |
20 |
3 |
3 |
2 |
1 |
12 |
4 |
1 |
0 |
4 |
1 |
3 |
4 |
0 |
1 |
|
|
9 |
7 |
5 |
6 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
2 |
1 |
2 |
0 |
1 |
0 |
|
2 x1 + x2 + 4 x3 (r) max,
2 x1 + x2 + 2 x3 (r) min,
x1 + 3 x3 і 9;
x2 + 2 x3 Ј 8;
x1 + 2 x2 + x3 Ј 12;
a41 x1 + a42 x2 Ј b4 ;
x1 , x3, x2 і 0.