|
Задания к лабораторно-практическим работам |
|
|
3.4.1. Постановка задачи и применение в инженерном деле3.4.2. Методы штрафных функций3.4.3. Методы прямого поиска3.4.4. Методы линеаризации3.4.5. Контрольные вопросы и задания |
Задача решается с использованием пакета MathCAD (лесоинженеры) или любого алгоритмического языка (АСОИУ) с проверкой в пакете EXCEL или LINGO. В отчете отразить постановку задачи а также приложить распечатки созданных программ и тестовых решений. |
Рассмотрим конкретный пример задачи условного нелинейного программирования.
Пример 3.9. План выпуска мебели.
Предприятие может выпускать два вида корпусной мебели. На их изготовление идет древесина трех видов. Запасы древесины на предприятии, нормы их расхода aij (i=1,2,3; j=1,2), себестоимость сj и оптовые цены указаны в табл. 3. Из-за брака в процессе производства расход древесины зависит от объема xj производства изделий и в первом приближении выражается линейной функцией aij + xj , а себестоимость продукции - функцией cj + 0,1xj . Изделия могут выпускаться в любых соотношениях, так как сбыт обеспечен. Предприятие обязано с целью изучения спроса населения выпустить не менее двух комплектов каждого вида мебели. Составить план выпуска изделий, обеспечивающий получение максимальной прибыли.
Таблица 3.2.
|
Порода
|
Запас сырья, м3 |
Нормы расхода на изделие вида |
|
|
1 |
2 |
||
|
Сосна |
100 |
10 |
20 |
|
Береза |
120 |
20 |
20 |
|
Дуб |
150 |
20 |
20 |
|
Себестоимость, млн. руб. |
5 |
10 |
|
|
Цена, млн. руб. |
7 |
13 |
|
Из-за брака в процессе производства расход ресурсов зависит от объема
xj (j=1,2) производства изделий и в первом приближении выражается линейной функцией aij + xj, а себестоимость продукции - функцией cj + 0,1xj . Изделия могут выпускаться в любых соотношениях, так как сбыт обеспечен. Составить план выпуска изделий, обеспечивающий получение максимальной прибыли.Постановка задачи.
1. В качестве показателя эффективности целесообразно взять прибыль предприятия за операцию (в млн. руб.).
2. В качестве управляемых переменных задачи следует взять:
x1 - количество комплектов корпусной мебели 1;
x2 - количество комплектов корпусной мебели 2.
3. Целевая функция:
W = [
7 - (5+0,1x1)] x1 + [13 - (10+0,1x2)] x2 (r) max,или
W =
2x1 - 0,1x12 + 3x2 - 0,1x22.4. Ограничения:
4.1. По использованию сосны, м3:
(10+x1)
x1 + (20+x2)x2 Ј 100.4.2. По использованию березы, м3:
(20+x1)
x1 + (10+x2)x2 Ј 120.4.3. По использованию дуба, м3:
(20+x1)
x1 + (10+x2)x2 Ј 150.4.4. Обязательства по контракту, шт.:
x1
і 2.4.5. Областные ограничения:
x2
і 2.Задача сводится к нахождению неотрицательных
x1* и x2*, удовлетворяющих нелинейным ограничениям и доставляющих максимум нелинейной целевой функции.Задачи нелинейной оптимизации (условной многопараметрической оптимизации) подразделяют следующим образом:
3.4.2. Методы штрафных функций
С помощью штрафных функций
P(x,R) = W(x) + W (R,g(x),h(x)), (3.18)
где
R - набор штрафных параметров;
W - штраф,
исходная задача условной оптимизации преобразуется в последовательность задач безусловной оптимизации. Штраф W определяется так, чтобы допустимые точки задачи имели преимущество перед недопустимыми в отношении безусловной оптимизации штрафной функции. Здесь штраф как бы создает вдоль границы допустимой области барьер из бесконечно больших значений функции P.
К штрафу выдвигаются следующие требования:
Методы штрафных функций классифицируются в соответствии со способами учета ограничений - неравенств g(x), так как ограничения-равенства h(x) учитываются во всех методах одинаково с помощью квадратичного штрафа
W
= R{h(x)}2. (3.19)При рассмотрении любой штрафной функции требуется выбрать начальное значение R и изменять его после решения каждой подзадачи безусловной оптимизации с тем, чтобы обеспечить сходимость. Для квадратичного штрафа, учитывающего ограничения - равенства, представляется целесообразным начинать с R=0, а затем последовательно увеличивать R на некоторое
D R или использовать возрастающие степени какого-либо числа, например 10. В результате получаемые точки будут все точнее и точнее удовлетворять ограничениям.Для учета ограничений - неравенств используют следующие штрафы:
W
= 1020 , (3.20)
, (3.20)
где
![]() - множество индексов нарушенных ограничений gj(x)<0 при j
- множество индексов нарушенных ограничений gj(x)<0 при j
W
= -R ln[g(x)]. (3.21)Отрицательный штраф исключают положив
W
= R [1/g(x)]. (3.22)Итерации следует начинать с начальной допустимой точки при положительном R, значения которого в пределе должно стремиться к нулю.
W
= R [g(x)]2 , (3.23)где
g(x) = ![]()
В данном методе недопустимые точки не создают проблем (в отличие от предыдущих), поэтому он весьма удобен. Кроме того функция P(x,R) определена и непрерывна всюду. Вычисления следует проводить с положительными Ri; после решения очередной подзадачи безусловной оптимизации R необходимо увеличивать.
Алгоритм методов штрафных функций:
Шаг 1. Задать значения N, J, K,
e 1, e 2, e 3, xo, Ro,где
xo - начальное приближение для x*;
Ro - начальный выбор штрафных параметров.
Шаг 2. Построить P(x,R) = W(x) +
W (R,g(x),h(x)).Шаг 3. Найти xt+1 минимизирующее значение P(xt+1,Rt) при фиксированном Rt. В качестве начальной точки использовать xt, а в качестве параметра окончания шага - константу
e 2 (возможно и e 1).Шаг 4. Проверить, выполняется ли условие
|
P(xt+1,Rt)-P(xt,Rt-1) | Ј e 3.Шаг 5. Положить Rt+1=Rt+
D Rt в соответствии с используемым правилом пересчета, после чего вернуться к шагу 2.
В методах прямого поиска ограничения учитываются в явном виде. Необходимость разработки этих методов связана с тем, что в инженерных приложениях часто приходится сталкиваться с случаями, когда целевые функции не заданы в явном виде. Эти методы строятся на интуитивных соображениях, не подкреплены сторгой теорией и, следовательно, не гарантируется их сходимость. Несмотря на это, в силу своей логической простоты эти методы легко реализуются.
Перед непосредственным применением методов прямого поиска необходимо провести ряд мероприятий по подготовке задачи к решению, а именно
Простейший способ исключения ограничений в виде равенств заключается в решении его относительно одной из переменных с последующим исключением этой переменной путем подстановки полученного выражения в соотношения, описывающие задачу. При этом следует учитывать, что границы значений исключаемых переменных сохраняются в задаче в виде ограничений - неравенств.
Несмотря на то, что подстановка является самым простым способом исключения ограничений - равенств, не всегда оказывается возможным ее осуществить. В этом случае проблема решается путем численного решения уравнения относительно зависимых переменных при заданных значениях независимых оптимизирующих переменных.
Для определения начальной допустимой точки целесообразно использовать процедуру случайного поиска, основная идея которого будет рассмотрена ниже.
После проведения процедуры подготовки задачи к решению следует приметить один из методов условной оптимизации. Рассмотрим два метода прямого поиска:
Алгоритм:
Заданы границы значений всех переменных xiL, xiU, i=1,2,..., N (размерность задачи), допустимая точка xo, параметр отображения a (рекомендуется a =1,3) и параметры окончания вычислений e и d .
Шаг 1. Построение начального комплекса, состоящего из P допустимых точек(рекомендуется P=2N). Для каждой точки p = 1, 2,...,P-1
Шаг 2. Отражение комплекса:
Шаг 3. Корректировка для обеспечения допустимости:
Шаг 4. Проверка условий окончания вычислений:
Наиболее простой процедурой случайного поиска является прямая выборочная процедура, заключающаяся в разыгрывании на ЭВМ последовательности точек с координатами
xi = xiL +ri (xiU - xiL), i=1,2,...,N, (3.24)
где
ri - случайная величина, равномерно распределенная на интервале [0,1].
После проверки каждой точки на допустимость вычисляются значения целевой функции, которое сравнивается с наилучшим значением, полученным к данному моменту. Если текущая точка дает лучшее значение, то она запоминается, в противном - отбрасывается. Процесс прекращается после заданного числа итераций N или по исчерпанию заданного машинного времени. Для получения 90% доверительного интервала величиной e i (xiU - xiL), где 0<e <1, для переменной xi совместный случайный поиск требует
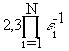
испытаний. При N=5,
e i=0,01 число испытаний оценивается в 2,3 1010, что исключает возможность непосредственного использования метода.Значительного увеличения эффективности процедуры случайного поиска можно достигнуть путем группировки выборок в серии. При этом наилучшая точка в каждой серии используется как начальная точка следующей серии, точки которой уже выбираются из интервала меньшей величины. Данная процедура получила название выборкой со сжатием пространства поиска. Рассмотрим более подробно ее алгоритм.
Заданы границы значений всех переменных xiL, xiU, i=1,2,..., N (размерность задачи), начальные допустимая точка xo и интервал поиска
D xo = xiU - xiL, количество серий Q, количество точек в серии P и параметр окончания вычислений e . Для каждой из серий, начиная с q = 1, необходимо выполнить следующие действия.Шаг 1. Для i = 1,2,...,N вычислить
xip = xiq-1 +ri
D xq-1,где
ri - случайная величина, равномерно распределенная на интервале [-0,5,0,5].
Шаг 2.
Шаг 3. Уменьшить интервал поиска, полагая
D xiq = e i D xiq-1.Шаг 4.
Идея методов заключается в сведении задачи нелинейного программирования к задаче линейного программирования. С этой целью нелинейные функции целевой функции W(x) и ограничений g(x), h(x) в ряд Тейлора до членов первого порядка в окрестности точки линеаризации xt, что позволяет W(x), g(x), h(x) аппроксимировать линейными функциями и свести общую задачу нелинейного программирования
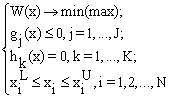
к следующей задаче линейного программирования
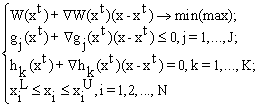
Решая ее при помощи методов линейного программирования, находим новое приближение xt+1. В случае нелинейных функций точка xt+1 обычно недопустимая точка. Однако для сходимости к оптимуму достаточно, чтобы последовательность точек {xt}, полученных в результате решения последовательности подзадач линейного программирования, выполнялось следующее условие: значение целевой функции W и невязки по ограничениям в xt+1 меньше их значений в точке xt.
3.4.5. Контрольные вопросы и задания